Transformations élémentaires des matrices et leurs propriétés. Algèbre matricielle - transformations élémentaires de matrices Transformations élémentaires du déterminant d'une matrice

Les trois opérations suivantes sont appelées transformations élémentaires des lignes de la matrice:

1) Multiplications ième ligne matrices pour le nombre λ ≠ 0 :

que nous écrirons sous la forme (i) → λ(i).

2) Permutation de deux lignes dans une matrice, par exemple la i-ème et la k-ème lignes :

que nous écrirons sous la forme (i) ↔ (k).

3) Ajouter à la i-ème ligne de la matrice sa k-ème ligne de coefficient λ :

que nous écrirons sous la forme (i) → (i) + λ(k).

Des opérations similaires sur les colonnes matricielles sont appelées transformations de colonnes élémentaires.

Chaque transformation élémentaire des lignes ou des colonnes d'une matrice a transformation élémentaire inverse, qui transforme la matrice transformée en celle d'origine. Par exemple, la transformation inverse pour permuter deux chaînes consiste à permuter les mêmes chaînes.

Chaque transformation élémentaire des lignes (colonnes) de la matrice A peut être interprétée comme une multiplication de A à gauche (à droite) par une matrice d'un type particulier. Cette matrice est obtenue si la même transformation est effectuée sur matrice d'identité. Examinons de plus près les conversions de chaînes élémentaires.

Soit la matrice B le résultat i-ème multiplication lignes d'une matrice A de type m×n par le nombre λ ≠ 0. Alors B = E i (λ)A, où la matrice E i (λ) est obtenue à partir de la matrice identité E d'ordre m en multipliant son i- ème ligne par le nombre λ.

Soit la matrice B obtenue à la suite de la permutation des ième et kième lignes de la matrice A de type m×n. Alors B = F ik A, où la matrice F ik est obtenue à partir de la matrice identité E d'ordre m en réorganisant ses i-ième et k-ième lignes.

Soit la matrice B obtenue en ajoutant sa kème ligne de coefficient λ à la i-ème ligne d'une matrice m×n A. Alors B = G ik (λ)А, où la matrice G ik est obtenue à partir de la matrice identité E d'ordre m en ajoutant la k-ème ligne avec le coefficient λ à la i-ème ligne, c'est-à-dire à l'intersection de la i-ème ligne et de la k-ème colonne de la matrice E, l'élément zéro est remplacé par le nombre λ.

Les transformations élémentaires des colonnes de la matrice A sont mises en œuvre exactement de la même manière, mais en même temps elles sont multipliées par des matrices d'un type spécial non pas à gauche, mais à droite.

Grâce à des algorithmes basés sur des transformations élémentaires de lignes et de colonnes, les matrices peuvent être transformées sous différentes formes. L’un des algorithmes les plus importants constitue la base de la preuve du théorème suivant.

Théorème 10.1. En utilisant des transformations élémentaires de lignes, n'importe quelle matrice peut être réduite à vue en escalier.

◄ La preuve du théorème consiste à construire un algorithme spécifique de réduction de la matrice sous forme échelonnée. Cet algorithme consiste à répéter de manière répétée dans un certain ordre trois opérations associées à un élément actuel de la matrice, sélectionné en fonction de son emplacement dans la matrice. À la première étape de l'algorithme, nous sélectionnons celui en haut à gauche comme élément actuel de la matrice, c'est-à-dire [UNE] 11 .

1*. Si l'élément courant est nul, passez à l'opération 2*. S'il n'est pas égal à zéro, alors la ligne dans laquelle se trouve l'élément actuel (la ligne actuelle) est ajoutée avec les coefficients appropriés aux lignes situées en dessous, de sorte que tous les éléments matriciels de la colonne sous l'élément actuel deviennent nuls. Par exemple, si l'élément actuel est [A] ij , alors comme coefficient pour la k-ième ligne, k = i + 1, ... , nous devrions prendre le nombre - [A] kj /[A] ij . Nous sélectionnons un nouvel élément actuel, en nous déplaçant dans la matrice d'une colonne vers la droite et d'une ligne vers le bas, et passons à l'étape suivante, en répétant l'opération 1*. Si un tel changement n'est pas possible, c'est-à-dire la dernière colonne ou ligne a été atteinte, on arrête la transformation.

2*. Si l'élément actuel dans une ligne de la matrice est égal à zéro, alors nous parcourons les éléments de la matrice situés dans la colonne sous l'élément actuel. S'il n'y en a pas non nul parmi eux, on passe à l'opération 3*. Laisser entrer kème ligne il y a un élément non nul en dessous de l'élément actuel. Échangez le courant et kème ligne et retour à l'opération 1*.

3*. Si l'élément courant et tous les éléments en dessous (dans la même colonne) sont égaux à zéro, nous changeons l'élément courant en déplaçant une colonne vers la droite dans la matrice. Si un tel décalage est possible, c'est-à-dire que l'élément courant n'est pas dans la colonne la plus à droite de la matrice, alors on répète l'opération 1*. Si nous avons déjà atteint le bord droit de la matrice et que la modification de l'élément actuel est impossible, alors la matrice a une forme échelonnée et nous pouvons arrêter la transformation.

Puisque la matrice est finie dimensions, et en une étape de l'algorithme, la position de l'élément actuel est décalée vers la droite d'au moins une colonne, le processus de transformation se terminera, et en pas plus de n étapes (n est le nombre de colonnes dans la matrice). Cela signifie qu'un moment viendra où la matrice aura une forme en escalier.

Exemple 10.10. Transformons la matrice sous forme échelonnée en utilisant des transformations de chaînes élémentaires.

En utilisant l'algorithme de la preuve du théorème 10.1 et en écrivant les matrices après avoir terminé ses opérations, on obtient

Les transformations élémentaires sont les actions suivantes sur les lignes et colonnes de la matrice A :

1) échanger deux lignes ou colonnes d'une matrice ;

2) multiplier une ligne ou une colonne d'une matrice par un nombre autre que zéro ;

3) ajouter une autre ligne (colonne) à une ligne (colonne).

Théorème. Les transformations élémentaires ne changent pas le rang de la matrice, c'est-à-dire que si la matrice B est obtenue à partir de la matrice A par des transformations élémentaires, alors.

Preuve. 1). Lors de l'échange de deux colonnes d'une matrice, le nombre maximum de colonnes linéairement indépendantes ne change pas, et donc son rang ne change pas.

2). Supposons que la matrice B soit obtenue à partir de la matrice A en multipliant la i-ème ligne par le nombre t0 et r(A) =k. Évidemment, tout mineur de la matrice B qui ne contient pas la ième ligne est égal au mineur correspondant de la matrice A, et tout mineur de la matrice B contenant la ième ligne est égal au mineur correspondant de la matrice A multiplié par le nombre t. Par conséquent, le mineur d'ordre k de la matrice B, correspondant à la base mineure de la matrice A, sera non nul, et tous les mineurs d'ordre k+1 de la matrice B, ainsi que tous les mineurs d'ordre k+1 de la matrice A, sera égal à zéro. Cela signifie que r(B)=k=r(A).

3). Soit la matrice B être obtenue à partir de la matrice A en ajoutant la i-ème ligne à la j-ème ligne et r(A) = k. Les mineurs d'ordre k+1 de la matrice B qui ne contiennent pas la j-ème ligne seront égaux aux mineurs correspondants de la matrice A, et donc égaux à zéro. Les mineurs d'ordre k+1 de la matrice B contenant les ième et jième lignes seront égaux à la somme de deux déterminants nuls. L'un de ces déterminants contient deux lignes identiques (la j-ème ligne contient les éléments de la i-ème ligne), et le deuxième déterminant est un mineur d'ordre k+1 de la matrice A et est donc égal à zéro. Les mineurs d'ordre k+1 de la matrice B, contenant la j-ème ligne, mais ne contenant pas la i-ème ligne, seront égaux à la somme de deux mineurs d'ordre k+1 de la matrice A et seront donc également égaux à zéro. Par conséquent, tous les mineurs d’ordre k+1 de la matrice B sont égaux à 0 et r(B)k=r(A).

Supposons que la matrice C soit obtenue à partir de la matrice B en multipliant la i ligne par (-1). Ensuite, la matrice A est obtenue à partir de la matrice C en ajoutant la i-ème ligne à la j-ème ligne et en multipliant la i-ème ligne par (-1). Par conséquent, comme démontré ci-dessus, il y aura r(A)r(C) =r(B). Ainsi, les inégalités r(B)r(A) et r(A)r(B) sont simultanément valables, ce qui signifie que r(A) =r(B).

Cette propriété des transformations élémentaires est utilisée en pratique pour calculer le rang d'une matrice. Pour ce faire, à l'aide de transformations élémentaires, on réduit cette matrice (non nulle) A à une forme trapézoïdale, c'est-à-dire à la forme

B = ,

où éléments pour tout i = 1,2,...,k; éléments pour tout i > j et

je > k. Évidemment, r(B) = k, c'est-à-dire que le rang de la matrice B est égal au nombre de lignes non nulles. Cela découle du fait que le mineur d'ordre k de la matrice B, situé à l'intersection des k premières lignes et colonnes, est un déterminant diagonal et est égal à ; et tout mineur d'ordre k+1 de la matrice B contient une ligne nulle, ce qui signifie qu'il est égal à 0 (ou, si k = n, il n'y a pas de tels mineurs du tout).

Théorème. Toute matrice A non nulle de dimension mn peut être réduite à une forme trapézoïdale à l'aide de transformations élémentaires.

Preuve. Puisque A0, alors il existe un élément matriciel
. En échangeant la première et la ième ligne, la première et la j-ième colonne, on déplace l'élément dans le coin supérieur gauche de la matrice et désignent
. Puis à la i-ième ligne de la matrice résultante (i= 2,3, ...,m) on ajoute la première ligne multipliée par le nombre . Grâce à ces transformations élémentaires, on obtient la matrice

UN
.

Si tous les éléments
les matrices A sont égales à zéro, alors le théorème est prouvé. S'il y a un élément
, puis, en réorganisant les deuxième et ième lignes, les deuxième et j-ième colonnes de la matrice A, on déplace l'élément à la place de l'élément et désigne
(Si
, alors on note immédiatement
). Ensuite, à la i-ème ligne de la matrice résultante (i= 3, ...,m), nous ajoutons la deuxième ligne multipliée par le nombre . En conséquence, nous obtenons la matrice

En poursuivant ce processus, en un nombre fini d'étapes, nous obtenons la matrice B, c'est-à-dire que nous réduisons la matrice A à une forme trapézoïdale.

Exemple. Calculons le rang de la matrice



. Les flèches indiquent les transformations élémentaires suivantes : 1) les première et deuxième lignes ont été interverties ; 2) ajouté une troisième à la quatrième ligne ; 3) ajouté la première ligne, multipliée par -2, à la troisième ligne et divisé la quatrième ligne par 3 ; 4) divisé la troisième ligne par 5 et interverti les troisième et quatrième lignes ; 5) une deuxième ligne a été ajoutée à la troisième ligne, multipliée par -3, et une troisième a été ajoutée à la quatrième ligne. On voit que la matrice obtenue à partir de la matrice A par les transformations élémentaires indiquées a une forme trapézoïdale à trois lignes non nulles. Donc r(A) = 3.

Les transformations matricielles élémentaires comprennent :

1. Modification de l'ordre des lignes (colonnes).

2. Suppression de zéro lignes (colonnes).

3. Multiplier les éléments de n'importe quelle ligne (colonne) par un nombre.

4. Ajouter aux éléments de n'importe quelle ligne (colonne) les éléments d'une autre ligne (colonne), multipliés par un nombre.

Systèmes d'équations algébriques linéaires (Concepts et définitions de base).

1. Système méquations linéaires avec n appelés inconnus système d'équations de la forme :

2.Par décision le système d'équations (1) est appelé une collection de nombres X 1 , X 2 , … , X n , transformer chaque équation du système en une identité.

3. Le système d'équations (1) est appelé articulation, s'il a au moins une solution ; si un système n'a pas de solutions, on l'appelle non conjoint.

4. Le système d'équations (1) est appelé certain, s'il n'a qu'une seule solution, et incertain, s'il a plus d'une solution.

5. À la suite de transformations élémentaires, le système (1) est transformé en un système équivalent (c'est-à-dire ayant le même ensemble de solutions).

Aux transformations élémentaires les systèmes d'équations linéaires comprennent :

1. Suppression des lignes nulles.

2. Changer l'ordre des lignes.

3. Ajouter aux éléments d'une ligne les éléments d'une autre ligne, multipliés par un nombre.

Méthodes de résolution de systèmes d'équations linéaires.

1) Méthode matricielle inverse (méthode matricielle) pour résoudre des systèmes de n équations linéaires à n inconnues.

Système néquations linéaires avec n appelés inconnus système d'équations de la forme :

Écrivons le système (2) sous forme matricielle ; pour cela nous introduisons la notation.

Matrice de coefficients pour les variables :

X = est une matrice de variables.

B = est une matrice de termes libres.

Alors le système (2) prendra la forme :

UN× X = B– équation matricielle.

En résolvant l'équation, on obtient :

X = UN -1 × B

Exemple:

; ;

1) │A│= 15 + 8 ‒18 ‒9 ‒12 + 20 = 4  0 la matrice A -1 existe.

Ã =

4) A -1 = × Ã = ;

X = A-1 × B

Répondre:

2) Règle de Cramer pour résoudre des systèmes de n – équations linéaires avec n – inconnues.

Considérons un système de 2 – x équations linéaires à 2 – inconnues :

Résolvons ce système en utilisant la méthode de substitution :

De la première équation il résulte :

En substituant dans la deuxième équation, on obtient :

En substituant la valeur dans la formule pour, nous obtenons :

Le déterminant Δ est le déterminant de la matrice système ;

Δ X 1 - déterminant de la variable X 1 ;

Δ X 2 - déterminant de la variable X 2 ;

Formules :

X 1 =;X 2 =;…,X n = ;Δ  0;

- sont appelés Les formules de Cramer.

Lors de la recherche de déterminants d'inconnues X 1 , X 2 ,…, X n la colonne de coefficients de la variable dont le déterminant est trouvé est remplacée par une colonne de termes libres.

Exemple: Résoudre un système d'équations en utilisant la méthode de Cramer

Solution:

Composons et calculons d'abord le déterminant principal de ce système :

Puisque Δ ≠ 0, le système a une solution unique, qui peut être trouvée en utilisant la règle de Cramer :

où Δ 1, Δ 2, Δ 3 sont obtenus à partir du déterminant de Δ en remplaçant respectivement la 1ère, la 2ème ou la 3ème colonne par la colonne des termes libres.

Ainsi:

Méthode de Gauss pour résoudre des systèmes d'équations linéaires.

Considérez le système :

La matrice étendue du système (1) est une matrice de la forme :

Méthode Gauss est une méthode d'élimination séquentielle des inconnues des équations du système, en commençant par la deuxième équation jusqu'à m- cette équation.

Dans ce cas, au moyen de transformations élémentaires, la matrice du système est réduite à triangulaire (si m = n et déterminant du système ≠ 0) ou par étapes (si m< n ) formulaire.

Ensuite, à partir de la dernière équation par nombre, toutes les inconnues sont trouvées.

Algorithme de la méthode Gauss :

1) Créez une matrice étendue du système, comprenant une colonne de termes libres.

2) Si UN 11  0, puis divisez la première ligne par UN 11 et multiplier par (– un 21) et ajoutez la deuxième ligne. De même atteindre m-cette ligne :

Page 1 diviser par UN 11 et multiplier par (– UN m 1) et ajoutez m– cette page

De plus, à partir des équations, à partir de la seconde jusqu'à m– c'est-à-dire que la variable sera exclue X 1 .

3) A la 3ème étape, la deuxième ligne est utilisée pour des transformations élémentaires similaires des lignes de la 3ème à m- Tuyu. Cela éliminera la variable X 2, à partir de la 3ème ligne jusqu'à m– tuyu, etc.

À la suite de ces transformations, le système sera réduit à une forme triangulaire ou en escalier (dans le cas d'une forme triangulaire, il y aura des zéros sous la diagonale principale).

Réduire un système à une forme triangulaire ou étagée est appelé méthode gaussienne directe, et trouver des inconnues dans le système résultant est appelé en marche arrière.

Exemple:

Déménagement direct. Présentons la matrice étendue du système

en utilisant des transformations élémentaires pour former par étapes. Réorganisons les première et deuxième lignes de la matrice UN b, on obtient la matrice :

Ajoutons la deuxième ligne de la matrice résultante avec la première, multipliée par (‒2), et sa troisième ligne avec la première ligne, multipliée par (‒7). Obtenons la matrice

À la troisième ligne de la matrice résultante, nous ajoutons la deuxième ligne, multipliée par (‒3), ce qui donne une matrice en étapes

Ainsi, nous avons réduit ce système d'équations à une forme pas à pas :

Mouvement inversé. À partir de la dernière équation du système d'équations pas à pas résultant, nous trouvons séquentiellement les valeurs des inconnues :

La matrice de transformation permet de calculer les nouvelles coordonnées d'un objet lors de sa transformation. En modifiant les valeurs des éléments de la matrice de transformation, toutes les transformations peuvent être appliquées aux objets (par exemple : mise à l'échelle, mise en miroir, rotation, déplacement, etc.). Lors de toute transformation, le parallélisme des lignes de l'objet est conservé.

Les coordonnées en PDF sont exprimées en termes d'espace bidimensionnel. Un point (x, y) dans l'espace peut être exprimé sous forme vectorielle . Le troisième élément constant de ce vecteur (1) est nécessaire pour utiliser le vecteur à matrices 3x3 dans les calculs décrits ci-dessous.

La transformation entre deux systèmes de coordonnées est représentée sous la forme d'une matrice 3x3 et s'écrit comme suit :

Les transformations de coordonnées sont exprimées sous forme de multiplications matricielles :

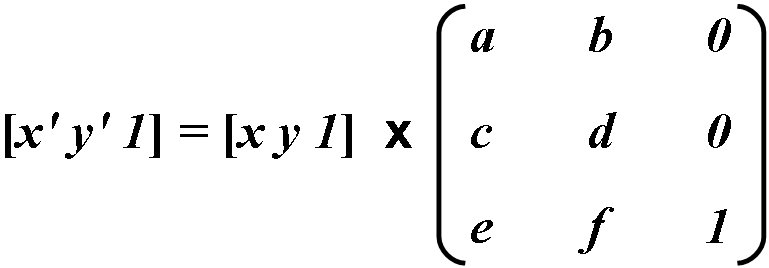
La dernière colonne n’ayant aucune influence sur les résultats des calculs, elle ne participe pas aux calculs. Les coordonnées de transformation sont calculées à l'aide des formules suivantes :

Matrice d'identité

Une matrice d'identité est celle dont les valeurs matricielles un Et dégal 1 , et le reste est égal 0 . Cette matrice est utilisée par défaut, puisqu'elle n'entraîne pas de transformation. Par conséquent, la matrice d'identité sert de base.

Mise à l'échelle

Pour augmenter ou diminuer la taille horizontale/verticale d'un objet, modifiez la valeur un ou d en conséquence, et appliquez le reste de la matrice d’identité.

Par exemple: Pour doubler la taille d'un objet horizontalement, il faut prendre la valeur de a égale à 2, et le reste doit être laissé tel quel dans la matrice d'identité.

Réflexion

Pour obtenir une image miroir horizontale d'un objet, définissez la valeur une = -1, verticalement d = -1. La modification des deux valeurs permet d'afficher à la fois horizontalement et verticalement.

Inclinaison

L'inclinaison de l'objet verticalement/horizontalement est assurée en changeant les valeurs b Et c respectivement. Changer la valeur b/-b- inclinaison haut/bas, c/-c- droite gauche.

Par exemple: Pour incliner l'objet verticalement vers le haut, définissez la valeur b = 1

On calcule les nouvelles coordonnées de l'objet :

De ce fait, seule la coordonnée conduit à l'inclinaison de l'objet oui, qui augmente de la valeur X.

Tourner

La rotation est une combinaison de mise à l'échelle et d'inclinaison, mais pour conserver les proportions originales d'un objet, la transformation doit être effectuée avec des calculs précis utilisant des sinus et des cosinus.

La rotation elle-même se produit dans le sens inverse des aiguilles d'une montre, α spécifie l'angle de rotation en degrés.

En mouvement

Le déplacement se fait en changeant les valeurs e(horizontalement) et F(verticalement). Les valeurs sont spécifiées en pixels.

Par exemple: Le déplacement à l'aide d'une matrice est rarement utilisé du fait que cette opération peut être effectuée par d'autres méthodes, par exemple en changeant la position d'un objet dans un onglet.

Étant donné que la matrice de transformation ne comporte que six éléments pouvant être modifiés, elle est affichée visuellement au format PDF. . Une telle matrice peut représenter n'importe quelle transformation linéaire d'un système de coordonnées à un autre. Les matrices de transformation sont formées comme suit :

Les mouvements sont indiqués comme , Où t x Et t y— les distances à partir de l'axe du système de coordonnées respectivement horizontalement et verticalement.
La mise à l'échelle est spécifiée comme . Cela met à l'échelle les coordonnées de sorte qu'une unité dans les dimensions horizontales et verticales dans le nouveau système de coordonnées ait la même taille que s x Et s y unités dans l’ancien système de coordonnées, respectivement.
Les rotations sont effectuées par la matrice , ce qui correspond à la rotation des axes du système de coordonnées de θ degrés dans le sens antihoraire.
La pente est indiquée comme , qui correspond à l'inclinaison de l'axe Xà un angle α et essieux ouià un angle β .

La figure ci-dessous montre des exemples de transformation. Les sens de mouvement, l'angle de rotation et l'inclinaison indiqués sur la figure correspondent aux valeurs positives des éléments matriciels.

Les multiplications matricielles ne sont pas commutatives : l'ordre dans lequel les matrices sont multipliées est important.

Le tableau ci-dessous montre les transformations et valeurs matricielles valides.

Dessin original	Dessin transformé	Matrice	Description
		1 0 0 2 0 0	Échelle verticale. Si la valeur matricielle est supérieure à 1, l'objet se dilate, inférieure à 1, il se contracte.
		2 0 0 1 0 0	Échelle horizontale. Si la valeur matricielle est supérieure à 1, l'objet se dilate, inférieure à 1, il se contracte.
		-1 0 0 1 0 0	Réflexion horizontale.
		1 0 0 -1 0 0	Réflexion verticale.
		1 1 0 1 0 0	Inclinaison verticale vers le haut.
		1 -1 0 1 0 0	Inclinaison verticale vers le bas.
		1 0 1 1 0 0	Inclinaison horizontale vers la droite.
		1 0 -1 1 0 0

Introduisons la notion de matrice élémentaire.

DÉFINITION. Une matrice carrée obtenue à partir de la matrice identité à la suite d'une transformation élémentaire non particulière sur les lignes (colonnes) est appelée matrice élémentaire correspondant à cette transformation.

Ainsi, par exemple, les matrices élémentaires du second ordre sont les matrices

où A est n’importe quel scalaire non nul.

La matrice élémentaire est obtenue à partir de la matrice identité E à la suite de l'une des transformations non singulières suivantes :

1) multiplier une ligne (colonne) de la matrice E par un scalaire non nul ;

2) ajouter (ou soustraire) à n'importe quelle ligne (colonne) de la matrice E une autre ligne (colonne) multipliée par un scalaire.

Désignons par la matrice obtenue à partir de la matrice E en multipliant la ligne par un scalaire non nul A :

Désignons par la matrice obtenue à partir de la matrice E en ajoutant (soustrayant) à une ligne une ligne multipliée par A ;

Notons la matrice obtenue à partir de la matrice identité E suite à l'application d'une transformation élémentaire sur les lignes ; il existe donc une matrice correspondant à la transformation

Considérons quelques propriétés des matrices élémentaires.

PROPRIÉTÉ 2.1. Toute matrice élémentaire est inversible. L'inverse d'une matrice élémentaire est élémentaire.

Preuve. La vérification directe montre que pour tout scalaire A. non nul et arbitraire, les égalités sont valables

Sur la base de ces égalités, nous concluons que la propriété 2.1 est vérifiée.

PROPRIÉTÉ 2.2. Le produit de matrices élémentaires est une matrice inversible.

Cette propriété découle directement de la propriété 2.1 et du corollaire 2.3.

PROPRIÉTÉ 2.3. Si une transformation élémentaire non singulière par lignes transforme la -matrice A en matrice B, alors . La déclaration d’obscénité est également vraie.

Preuve. S'il y a multiplication d'une chaîne par un scalaire A non nul, alors

Si donc

Il est facile de vérifier que l’inverse est également vrai.

PROPRIÉTÉ 2.4. Si la matrice C est obtenue à partir de la matrice A en utilisant une chaîne de transformations élémentaires non singulières par lignes, alors. L’inverse est également vrai.

Preuve. Par la propriété 2.3, la transformation transforme la matrice A en matrice, transforme la matrice en matrice, etc. Enfin, transforme la matrice en matrice Donc, .

Il est facile de vérifier que l’affirmation inverse est également vraie. Conditions d'inversibilité matricielle. Pour prouver le théorème 2.8, les trois lemmes suivants sont nécessaires.

LEMME 2.4. Une matrice carrée avec zéro ligne (colonne) est irréversible.

Preuve. Soit A une matrice carrée de ligne nulle, B une matrice quelconque, . Soit la ligne zéro de la matrice A ; Alors

c'est-à-dire que la i-ème ligne de la matrice AB est nulle. La matrice A est donc irréversible.

LEMME 2.5. Si les lignes d'une matrice carrée sont linéairement dépendantes, alors la matrice est irréversible.

Preuve. Soit A une matrice carrée avec des lignes linéairement dépendantes. Il existe ensuite une chaîne de transformations élémentaires en lignes non singulières qui transforment A en une matrice échelonnée ; laissez une telle chaîne. Par la propriété 2.4 des matrices élémentaires, l'égalité est vraie

où C est une matrice avec une ligne nulle.

Donc, d’après le lemme 2.4, la matrice C est irréversible. En revanche, si la matrice A était inversible, alors le produit de gauche dans l'égalité (1) serait une matrice inversible, comme le produit de matrices inversibles (voir corollaire 2.3), ce qui est impossible. La matrice A est donc irréversible.