Элементарные преобразования матриц и их свойства. Матричная алгебра - элементарные преобразования матриц Элементарные преобразования определителя матрицы

Следующие три операции называют элементарными преобразованиями строк матрицы :

1) Умножение i-й строки матрицы на число λ ≠ 0:

которое будем записывать в виде (i) → λ(i).

2) Перестановка двух строк в матрице, например i-й и k-й строк:

которую будем записывать в виде (i) ↔ (k).

3) Добавление к i-й строке матрицы ее k-й строки с коэффициентом λ:

что будем записывать в виде (i) → (i) + λ(k).

Аналогичные операции над столбцами матрицы называют элементарными преобразованиями столбцов .

Каждое элементарное преобразование строк или столбцов матрицы имеет обратное элементарное преобразование , которое преобразованную матрицу превращает в исходную. Например, обратным преобразованием для перестановки двух строк является перестановка тех же строк.

Каждое элементарное преобразование строк (столбцов) матрицы А можно трактовать как умножение A слева (справа) на матрицу специального вида. Эта матрица получается, если то же преобразование выполнить над единичной матрицей . Рассмотрим подробнее элементарные преобразования строк.

Пусть матрица B получается в результате умножения i-й строки матрицы A типа m×n на число λ ≠ 0. Тогда B = Е i (λ)А, где матрица Е i (λ) получается из единичной матрицы E порядка m умножением ее i-й строки на число λ.

Пусть матрица B получается в результате перестановки i-й и k-й строк матрицы А типа m×n. Тогда B = F ik А, где матрица F ik получается из единичной матрицы E порядка m перестановкой ее i-й и k-й строк.

Пусть матрица B получается в результате добавления к i-й строке матрицы А типа m×n ее k-й строки с коэффициентом λ. Тогда B = G ik (λ)А, где матрица G ik получается из единичной матрицы E порядка m в результате добавления к i-й строке k-й строки с коэффициентом λ, т.е. на пересечении i-й строки и k-го столбца матрицы E нулевой элемент заменен на число λ.

Точно так же реализуются элементарные преобразования столбцов матрицы A, но при этом она умножается на матрицы специального вида не слева, а справа.

С помощью алгоритмов, которые основаны на элементарных преобразованиях строк и столбцов, матрицы можно преобразовывать к различному виду. Один из важнейших таких алгоритмов составляет основу доказательства следующей теоремы.

Теорема 10.1. С помощью элементарных преобразований строк любую матрицу можно привести к ступенчатому виду .

◄ Доказательство теоремы состоит в построении конкретного алгоритма приведения матрицы к ступенчатому виду. Этот алгоритм состоит в многократном повторении в определенном порядке трех операций, связанных с некоторым текущим элементом матрицы, который выбирается исходя из расположения в матрице. На первом шаге алгоритма в качестве текущего элемента матрицы выбираем верхний левый, т.е. [A] 11 .

1*. Если текущий элемент равен нулю, переходим к операции 2*. Если же он не равен нулю, то строку, в которой расположен текущий элемент (текущую строку), добавляем с соответствующими коэффициентами к строкам, расположенным ниже, так, чтобы все элементы матрицы, стоящие в столбце под текущим элементом, обратились в нуль. Например, если текущий элемент есть [A] ij , то в качестве коэффициента для k-й строки, k = i + 1, ... , нам следует взять число - [A] kj /[A] ij . Выбираем новый текущий элемент, смещаясь в матрице на один столбец вправо и на одну строку вниз, и переходим к следующему шагу, повторяя операцию 1*. Если такое смещение невозможно, т.е. достигнут последний столбец или строка, преобразования прекращаем.

2*. Если текущий элемент в некоторой строке матрицы равен нулю, то просматриваем элементы матрицы, расположенные в столбце под текущим элементом. Если среди них нет ненулевых, переходим к операции 3*. Пусть в k-й строке под текущим элементом находится ненулевой элемент. Меняем местами текущую и k-ю строки и возвращаемся к операции 1*.

3*. Если текущий элемент и все элементы под ним (в том же столбце) равны нулю, меняем текущий элемент, смещаясь в матрице на один столбец вправо. Если такое смещение возможно, т. е. текущий элемент находится не в самом правом столбце матрицы, то повторяем операцию 1* . Если же мы уже достигли правого края матрицы и смена текущего элемента невозможна, то матрица имеет ступенчатый вид, и мы можем прекратить преобразования.

Так как матрица имеет конечные размеры , а за один шаг алгоритма положение текущего элемента смещается вправо хотя бы на один столбец, процесс преобразований закончится, причем не более чем за n шагов (n - количество столбцов в матрице). Значит, наступит момент, когда матрица будет иметь ступенчатый вид.

Пример 10.10. Преобразуем матрицу к ступенчатому виду с помощью элементарных преобразований строк.

Используя алгоритм из доказательства теоремы 10.1 и записывая матрицы после окончания выполнения его операций, получаем

Элементарными преобразованиями называют следующие действия над строками и столбцами матрицы A:

1) перестановку местами двух строк или столбцов матрицы;

2) умножение строки или столбца матрицы на число, отличное от нуля;

3) прибавление к одной строке (столбцу) другой строки (столбца).

Теорема. Элементарные преобразования не меняют ранг матрицы, то есть, если матрица B получена из матрицы A элементарными преобразованиями, то.

Доказательство. 1). При перестановке местами двух столбцов матрицы максимальное число линейно независимых столбцов не меняется, а значит, не меняется и её ранг.

2). Пусть матрица Bполучена из матрицыAумножениемi- ой строки на числоt0 иr(A) =k. Очевидно, любой минор матрицыB, не содержащийi- тую строку, равен соответствующему минору матрицыA, а любой минор матрицыB, содержащийi-тую строку, равен соответствующему минору матрицыAумноженному на числоt. Следовательно, минор порядкаkматрицыB, соответствующий базисному минору матрицыA, будет отличен от нуля, а все миноры порядкаk+1 матрицыB, как и все миноры порядкаk+1 матрицыA, будут равны нулю. А это значит, чтоr(B)=k=r(A).

3). Пусть матрица Bполучена из матрицыAприбавлениемi- ой строки кj-той строке иr(A) =k. Миноры порядкаk+1 матрицыB, не содержащиеj-тую строку, будут равны соответствующим минорам матрицыA, и поэтому равны нулю. Миноры порядкаk+1 матрицыB, содержащиеi- тую иj-тую строки, будут равны сумме двух нулевых определителей. Один из этих определителей содержит две одинаковых строки (вj-той строке расположены элементыi–той строки), а второй определитель является минором порядкаk+1 матрицыAи поэтому равен нулю. Миноры порядкаk+1 матрицыB, содержащиеj-тую строку, но не содержащиеi-тую строку, будут равны сумме двух миноров порядкаk+1 матрицыAи поэтому тоже будут равны нулю. Следовательно, все миноры порядкаk+1 матрицыBравны 0 иr(B)k=r(A).

Пусть матрица Cполучена из матрицыBумножениемi–той строки на (-1). Тогда матрицаAполучается из матрицыCприбавлениемi–той строки кj-той строке и умножениемi–той строки на (-1). Следовательно, как было доказано выше, будетr(A)r(C) =r(B). Таким образом, одновременно справедливы неравенстваr(B)r(A) иr(A)r(B) откуда следует, чтоr(A) =r(B).

Это свойство элементарных преобразований используют на практике для вычисления ранга матрицы. Для этого, при помощи элементарных преобразований, приводят данную (ненулевую) матрицу A к трапецевидной форме, то есть к виду

B = ,

где элементы для всех i = 1,2,...,k; элементыдля всех i > j и

i > k. Очевидно, что r(B) = k, то есть ранг матрицы Bравен числу ненулевых строк. Это следует из того, что минор порядка k матрицыB, расположенный на пересечении первых k строк и столбцов, является определителем диагонального вида и равен; а любой минор порядка k+1 матрицы В содержит нулевую строку, а значит, равен 0 (либо, если k = n, таких миноров нет вообще).

Теорема. Любую ненулевую матрицуAразмерностиmnможно привести к трапецевидной форме при помощи элементарных преобразований.

Доказательство. Так какA0, то существует элемент матрицы
. Переставив местами первую иi-тую строки, первый иj-тый столбцы, переместим элементв левый верхний угол матрицы и обозначим
. Затем кi-той строке полученной матрицы (i= 2,3, …,m) прибавим первую строку, умноженную на число. В результате этих элементарных преобразований получим матрицу

A
.

Если все элементы
матрицыAравны нулю, то теорема доказана. Если же существует элемент
, то, перестановкой второй иi-той строк, второго иj-того столбцов матрицыA, переместим элементна место элементаи обозначим
(если
, тогда сразу обозначим
). Затем кi-той строке полученной матрицы (i= 3, …,m) прибавим вторую строку, умноженную на число. В результате получим матрицу

Продолжив этот процесс, за конечное число шагов получим матрицу B, то есть приведем матрицуAк трапецевидной форме.

Пример. Вычислим ранг матрицы



. Стрелками обозначены следующие элементарные преобразования: 1) переставили местами первую и вторую строки; 2) прибавили к четвертой строке третью; 3) прибавили к третьей строке первую, умноженную на -2, и четвертую строку поделили на 3; 4) поделили третью строку на 5 и переставили местами третью и четвертую строки; 5) к третьей строке, умноженной на -3, прибавили вторую строку и к четвертой строке прибавили третью. Видно, что матрица, полученная из матрицы А указанными элементарными преобразованиями, имеет трапецевидную форму с тремя ненулевыми строками. Следовательно, r(A) = 3.

К элементарным преобразованиям матрицы относятся:

1. Изменение порядка строк (столбцов).

2. Отбрасывание нулевых строк (столбцов).

3. Умножение элементов любой строки (столбца) на одно число.

4. Прибавление к элементам любой строки (столбца) элементов другой строки (столбца), умноженных на одно число.

Системы линейных алгебраических уравнений слу (Основные понятия и определения).

1. Системой m линейных уравнений с n неизвестными называется система уравнений вида:

2. Решением системы уравнений (1) называется совокупность чисел x 1 , x 2 , … , x n , обращающая каждое уравнение системы в тождество.

3. Система уравнений (1) называется совместной , если она имеет хотя бы одно решение; если система не имеет решений, она называется несовместной .

4. Система уравнений (1) называется определенной , если она имеет только одно решение, и неопределенной , если у нее более одного решения.

5. В результате элементарных преобразований система (1) преобразуется к равносильной ей системе (т.е. имеющей то же множество решений).

К элементарным преобразованиям систем линейных уравнений относятся:

1. Отбрасывание нулевых строк.

2. Изменение порядка строк.

3. Прибавление к элементам любой строки элементов другой строки, умноженных на одно число.

Методы решения систем линейных уравнений.

1) Метод обратной матрицы (матричный метод) решения систем n линейных уравнений с n неизвестными.

Системой n линейных уравнений с n неизвестными называется система уравнений вида:

Запишем систему (2) в матричном виде, для этого введем обозначения.

Матрица коэффициентов перед переменными:

X = ‒ матрица переменных.

В = ‒ матрица свободных членов.

Тогда система (2) примет вид:

A ×X = B ‒ матричное уравнение.

Решив уравнение, получим:

X = A -1 ×B

Пример:

; ;

1) │А│= 15 + 8 ‒18 ‒9 ‒12 + 20 = 4  0 матрицаА -1 существует.

Ã =

4) А -1 = × Ã =;

Х = А -1 × B

Ответ:

2) Правило Крамера решения систем n – линейных уравнений с n – неизвестными.

Рассмотрим систему 2 ‒ х линейных уравнений с 2 ‒ мя неизвестными:

Решим эту систему методом подстановки:

Из первого уравнения следует:

Подставив во второе уравнение, получим:

Подставляем значение в формулу для, получим:

Определитель Δ - определитель матрицы системы;

Δ x 1 - определитель переменной x 1 ;

Δ x 2 - определитель переменной x 2 ;

Формулы:

x 1 =;x 2 =;…,x n = ;Δ  0;

‒ называются формулами Крамера.

При нахождении определителей неизвестных х 1 , х 2 ,…, х n заменяется столбец коэффициентов при той переменной, определитель которой находят, на столбец свободных членов.

Пример: Решить систему уравнений методом Крамера

Решение:

Составим и вычислим сначала главный определитель этой системы:

Так как Δ ≠ 0, то система имеет единственное решение, которое можно найти по правилу Крамера:

где Δ 1 , Δ 2 , Δ 3 получаются из определителя Δ путем замены 1‒ го, 2 ‒ го или 3 ‒ го столбца, соответственно, на столбец свободных членов.

Таким образом:

Метод Гаусса решения систем линейных уравнений.

Рассмотрим систему:

Расширенной матрицей системы (1) называется матрица вида:

Метод Гаусса – это метод последовательного исключения неизвестных из уравнений системы, начиная со второго уравнения по m – тое уравнение.

При этом путем элементарных преобразований матрица системы приводится к треугольной (если m = n и определитель системы ≠ 0) или ступенчатой (если m < n ) форме.

Затем, начиная с последнего по номеру уравнения, находятся все неизвестные.

Алгоритм метода Гаусса:

1) Составить расширенную матрицу системы, включающую столбец свободных членов.

2) Если а 11  0, то первую строку делим на а 11 и умножаем на (– a 21) и прибавляем вторую строку. Аналогично дойти до m –той строки:

I стр. делим на а 11 и умножаем на (– а m 1) и прибавляем m – тую стр.

При этом из уравнений, начиная со второго по m – тое, исключится переменная x 1 .

3) На 3 ‒ м шаге вторая строка используется для аналогичных элементарных преобразований строк с 3 ‒ й по m – тую. При этом исключится переменная x 2 , начиная с 3 ‒ й строки по m – тую, и т. д.

В результате этих преобразований система приведется к треугольной или ступенчатой форме (в случае треугольной формы под главной диагональю нули).

Приведение системы к треугольной или ступенчатой форме называется прямым ходом метода Гаусса , а нахождение неизвестных из полученной системы называется обратным ходом .

Пример:

Прямой ход. Приведём расширенную матрицу системы

с помощью элементарных преобразований к ступенчатому виду. Переставим первую и вторую строки матрицыA b , получим матрицу:

Сложим вторую строку полученной матрицы с первой, умноженной на (‒2), а её третью строку – с первой строкой, умноженной на (‒7). Получим матрицу

К третьей строке полученной матрицы прибавим вторую строку, умноженную на (‒3), в результате чего получим ступенчатую матрицу

Таким образом, мы привели данную систему уравнений к ступенчатому виду:

Обратный ход. Начиная с последнего уравнения полученной ступенчатой системы уравнений, последовательно найдём значения неизвестных:

Матрица преобразований применяется для вычисления новых координат объекта при его трансформации. Изменяя значения элементов матрицы преобразования, к объектам можно применять любые трансформации (например: масштабирование, зеркальное отражение, поворот, перемещение и т. п.). При любой трансформации сохраняется параллельность линий объекта.

Координаты в PDF выражаются в терминах двумерного пространства. Точка (x, y) в пространстве может быть выражена в векторной форме . Постоянный третий элемент этого вектора (1) нужен для использования вектора с матрицами 3х3 в вычислениях, описанных ниже.

Преобразование между двумя системами координат представлено, как матрица 3х3 и записывается следующим образом:

Координатные преобразования выражаются в виде матричных умножений:

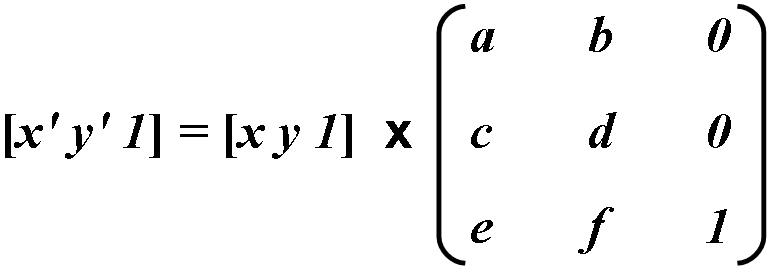
Так как последняя колонка не оказывает ни какого влияния на результаты расчета, то она в вычислениях не принимает участия. Координаты трансформации высчитываются по следующим формулам:

Единичная матрица

Единичной матрицей называется, та у которой значения матрицы a и d равны 1 , а остальные равны 0 . Такая матрица применяется по умолчанию, так как не приводит к трансформации. Поэтому единичную матрицу используют как основу.

Масштабирование

Для увеличения или уменьшения размера объекта по горизонтали/вертикали следует изменить значение a или d соответственно, а остальные применить из единичной матрицы.

Например: Для увеличения размера объекта в два раза по горизонтали, значение a необходимо принять равным 2, а остальные оставить такими как в единичной матрице.

Отражение

Чтобы получить зеркальное отображение объекта по горизонтали следует установить значение a = -1 , по вертикали d = -1 . Изменение обеих значений применяется для одновременного отображения по горизонтали и вертикали.

Наклон

Наклон объекта по вертикали/горизонтали обеспечивается изменением значений b и c соответственно. Изменение значения b/-b - наклон вверх/вниз, c/-c – вправо/влево.

Например: Для наклона объекта по вертикали вверх установим значение b = 1

Высчитываем новые координаты объекта:

В итоге к наклону объекта приводит только координата y , которая увеличивается на значение x .

Поворот

Поворот — это комбинация масштабирования и наклона, но для сохранения начальных пропорций объекта, преобразования должны проводится с точными вычислениями при использовании синусов и косинусов.

Сам поворот происходит против часовой стрелки, α задаёт угол поворота в градусах.

Перемещение

Перемещение осуществляется изменением значений e (по горизонтали) и f (по вертикали). Значения задаются в пикселях.

Например: Перемещение с использованием матрицы применяется редко из-за того, что эту операцию можно проделать другими методами, например, изменить положение объекта во вкладке .

Поскольку матрица трансформации имеет только шесть элементов, которые могут быть изменены, визуально она отображается в PDF . Такая матрица может представлять любое линейное преобразование из одной координатной системы в другую. Матрицы преобразований образуются следующим образом:

Перемещения указываются как , где t x и t y — расстояния от оси системы координат по горизонтали и вертикали, соответственно.
Масштабирование указывается как . Это масштабирует координаты так, что 1 единица в горизонтальном и вертикальном измерениях в новой координатной системе такого же размера, как и s x и s y единиц в старой координатной системе соответственно.
Повороты производятся матрицей , что соответствует повороту осей координатной системы на θ градусов против часовой стрелки.
Наклон указывается как , что соответствует наклону оси x на угол α и оси y на угол β .

На рисунке ниже показаны примеры трансформации. Направления перемещения, угол поворота и наклона, показанные на рисунке, соответствуют положительным значениям элементов матрицы.

Умножения матрицы не коммутативны — порядок, в котором перемножаются матрицы, имеет значение.

В таблице ниже приведены допустимые преобразования и значения матрицы.

Исходный рисунок	Трансформированный рисунок	Матрица	Описание
		1 0 0 2 0 0	Масштаб по вертикали. Если значение матрицы больше 1, объект расширяется, меньше 1 — сжимается.
		2 0 0 1 0 0	Масштаб по горизонтали. Если значение матрицы больше 1, объект расширяется, меньше 1 — сжимается.
		-1 0 0 1 0 0	Отражение по горизонтали.
		1 0 0 -1 0 0	Отражение по вертикали.
		1 1 0 1 0 0	Наклон по вертикали вверх.
		1 -1 0 1 0 0	Наклон по вертикали вниз.
		1 0 1 1 0 0	Наклон по горизонтали вправо.
		1 0 -1 1 0 0

Введем понятие элементарной матрицы.

ОПРЕДЕЛЕНИЕ. Квадратная матрица, получающаяся из единичной матрицы в результате неособенного элементарного преобразования над строками (столбцами), называется элементарной матрицей, соответствующей этому преобразованию.

Так, например, элементарными матрицами второго порядка являются матрицы

где А - любой ненулевой скаляр.

Элементарная матрица получается из единичной матрицы Е в результате одного из следующих неособенных преобразований:

1) умножение строки (столбца) матрицы Е на отличный от нуля скаляр;

2) прибавление (или вычитание) к какой-либо строке (столбцу) матрицы Е другой строки (столбца), умноженной на скаляр.

Обозначим через матрицу, получающуюся из матрицы Е в результате умножения строки на ненулевой скаляр А:

Обозначим через матрицу, получающуюся из матрицы Е в результате прибавления (вычитания) к строке строки, умноженной на А;

Через будем обозначать матрицу, получающуюся из единичной матрицы Е в результате применения элементарного преобразования над строками; таким образом, есть матрица, соответствующая преобразованию

Рассмотрим некоторые свойства элементарных матриц.

СВОЙСТВО 2.1. Любая элементарная матрица обратима. Матрица, обратная к элементарной, является элементарной.

Доказательство. Непосредственная проверка показывает, что для любого отличного от нуля скаляра А. и произвольных выполняются равенства

На основании этих равенств заключаем, что имеет место свойство 2.1.

СВОЙСТВО 2.2. Произведение элементарных матриц является обратимой матрицей.

Это свойство непосредственно следует из свойства 2.1 и следствия 2.3.

СВОЙСТВО 2.3. Если неособенное строчечное элементарное преобразование переводит -матрицу А в матрицу В, то . Верно и обрсипное утверждение.

Доказательство. Если есть умножение строки на ненулевой скаляр А, то

Если же , то

Легко проверить, что верно также обратное утверждение.

СВОЙСТВО 2.4. Если матрица С получается из матрицы А при помощи цепочки неособенных строчечных элементарных преобразований , то . Верно и обратное утверждение.

Доказательство. По свойству 2.3, преобразование переводит матрицу А в матрицу переводит матрицу в матрицу и т. д. Наконец, переводит матрицу в матрицу Следовательно, .

Легко проверить, что верно и обратное утверждение. Условия обратимости матрицы. Для доказательства теоремы 2.8 необходимы следующие три леммы.

ЛЕММА 2.4. Квадратная матрица с нулевой строкой (столбцом) необратима.

Доказательство. Пусть А - квадратная матрица с нулевой строкой, В - любая матрица, . Пусть - нулевая строка матрицы А; тогда

т. е. i-я строка матрицы АВ является нулевой. Следовательно, матрица А необратима.

ЛЕММА 2.5. Если строки квадратной матрицы линейно зависимы, то матрица необратима.

Доказательство. Пусть А - квадратная матрица с линейно зависимыми строками. Тогда существует цепочка неособенных строчечных элементарных преобразований, переводящих А в ступенчатую матрицу; пусть такая цепочка. По свойству 2.4 элементарных матриц, имеет место равенство

где С - матрица с нулевой строкой.

Следовательно, по лемме 2.4 матрица С необратима. С другой стороны, если бы матрица А была обратимой, то произведение слева в равенстве (1) было бы обратимой матрицей, как произведение обратимых матриц (см. следствие 2.3), что невозможно. Следовательно, матрица А необратима.